وبلاگ چت روم کامپیوتر و شبکه در سایت الفور

مهندسی اجتماعی Social Engineering
مقدمه :
اگر شما یک مدیر IT کاملا"فنی و تکنیکی هستید و در سازمان خود از تجهیزات سخت افزاری ونرم افزاری گران قیمت جهت برقراری امنیت شبکه استفاده می کنید ، وحتی اگر از تکنیکهای تحت شبکه آزمون نفوذ پذیری نیز بهره می برید باز هم ممکن است از شر افراد موسوم به مهندسان اجتماعی که از طریق کارکنان سازمان به اطلاعات مهم وحساس آن دست می یابند ، در امان نباشید .
همچنین اگر شما یک کارمند خوش خلق وکارا هستید وبا ارتباطات اجتماعی قوی بر قوانین خشک حاکم بر سازمان غلبه کرده وبدین وسیله در زمان کوتاهتر وظایف خود را به اتمام می رسانید و همواره از اجتماعی بودن سود برده اید ، باید بدانید که بیش از دیگران در معرض حملات مهندسان اجتماعی قرار دارید .
این مقاله در ابتدا به معرفی مهندسی اجتماعی و روشهای حمله توسط این نوع نفوذ گران پرداخته وسپس انواع سیاست گزاریهای مبتنی بر پیشگیری ومقابله با این نوع حملات را مورد بررسی قرار می دهد .
تعریف : مهندسی اجتماعی به مجموعه ای از تکنیکها اتلاق می شود که در آن از کاربران نا آگاه جهت انجام اعمال نفوذی یا فاش نمودن اطلاعات محرمانه سوء استفاده می شود . در این روش حمله گر یا نفوذ کننده در بیشتر موارد خود را پنهان نگاه داشته و از تماس رو در رو با طرف حمله اجتناب می نماید .
تکنیکهای مهندسی اجتماعی :
گاهی اوقات از تکنیکهای مهندسی اجتماعی تحت عنوان خطا های سخت افزاری انسان یاد می شود .
برخی از این تکنیکها عبارتند از :
این روش عبارتست از سناریو سازی ( بهانه جویی ) جهت اخذ اطلاعات ویا انجام عملی ناخواسته توسط فرد مورد هدف که عمدتا" از طریق تلفن صورت می پذیرد .
بهانه جویی چیزی بیش از یک دروغ ساده است ومی تواند با ادعای قانونی بودن تقاضای مورد نظر ، فرد را به دادن اطلاعاتی چون تاریخ تولد ، شماره و رمز حساب ویا حتی مبلغ آخرین فیش حقوقی و... ترغیب نماید .
امروز برنامه های Voice over IP استفاده از تکنیک Pretexting را ساده تر نموده اند چرا که رد یابی یک نفوذ گر از طریق آدرس IP به مراتب مشکل تر از خطوط تلفن است .
- روش سرقت هویت Phishing
این روش عبارتست از دستیابی به اطلاعات خصوصی وشخصی به صورت عوام فریبانه . در این روش نفوذ گر به
ارسال پست الکترونیکی از سوی یک شرکت معتبر پرداخته وتقاضای تائید اطلاعات را از طریق یک لینک وب
به ظاهر حقوقی می نماید و از این طریق کلیه اطلاعات شخصی از قبیل اسم ، مشخصات شناسنامه ای ،
آدرس منزل ، پست الکترونیک ورمز آن ، شماره حساب بانکی ورمز آن وسایراطلاعات را جهت سوء استفاده-
های بعدی اخذ می نماید .
گونه دیگر این تکنیک سرقت هویت به صورت تلفنی است که به جای لینک وب شماره تماسی به فرد داده می شود
وشماره مذکورعموما" با استفاده از منشی تلفنی خودکار از تماس گیرنده تقاضای ورود و یا تغییر کلمه رمز خود را
می نماید .
در این روش ضمیمه پست الکترونیکی فرستاده شده از سوی نفوذ گر آلوده به اسب تروجان بوده وبا بازشدن ضمیمه ، رایانه مورد نظر آماده نفوذ می گردد. نوع دیگری از اسبهای تروجان Road Apple نام داشته وعبارتند از هر گونه سخت افزار آلوده اعم از فلاپی ، دیسک فشرده ، حافظه Flash و ... که ممکن است با بر چسب های خاص ، کنجکاوی هر فرد عادی را نیز برانگیزند . در این روش حتی ممکن است سخت افزارهای مورد استفاده به صورت مجانی ویا اتفاقی سر راه فرد مورد نظر گذاشته شوند .
- روش مهندسی اجتماعی معکوس Quid Pro quo
در این روش نفوذ گر برخی مشکلات را به صورت مستقیم یا از طریق شبکه برای کامپیوتر کاربر ایجاد نموده وسپس
خود را به طریقی برای کمک وارد ماجرا می کند وبه این ترتیب علاوه بر جلب اعتماد کاربر به مقاصد خود به راحتی
دست می یابد.
در این روش از کاغذهای باطله ، مستندات بایگانی شده قدیمی ویا دیسکهای حاوی اطلاعات بایگانی شده جهت نفوذ استفاده می شود .
حال این سؤال مطرح می شود که چگونه شما می توانید در مقابل حملات مهندسی اجتماعی ایمن شوید ؟
اولین گام در این رابطه شناسایی راههای نفوذ وارائه راهکارهای مناسب در قالب سیاست گذاریهای سازمانی میباشد.بدیهی است هر نوع سیاست گذاری بدون ضمانت اجرایی در این زمینه راه به جایی نخواهد برد. . پس تمام اعضای مدیریت می بایست به طور آگاهانه این سیاستها را درک وسپس اجرایی نمایند .
در ذیل به برخی از این سیاستها که در ظاهر ساده اما کارا هستند می پردازیم:
1- عدم دسترسی مهمانان وبیگانگان به اسناد ، سیستم ها وسخت افزارها ی شرکت
2- اجرای طرح تکریم ارباب رجوع با دقت فراوان
- سیاستهای امحاء مستندات
1- انهدام کاغذهای کاری در دوره های مشخص ( تکه تکه کردن ، خرد کردن ، سوزاندن و....)
2- انهدام سخت افزار های حافظه در دوره های مشخص
- سیاستهای امنیت شبکه
1- محافظت فیزیکی از ابزارهای شبکه ورایانه ها
2- محافظت نرم افزاری از شبکه و برنامه ها
3- اعمال سیاستهای دقیق تهیه نسخ پشتیبان
- سیاستهای آموزش
1- آموزش نحوه شناسایی مهندسین اجتماعی به تمامی کارکنان
2- ایجاد پایگاه داده از انواع حملات موجود و رخ داده جهت تصمیم گیری های به موقع
- سیاستها ی پیشگیری ومقابله به صورت سازمان یافته
1- ایجاد واحد وشاغل خاص جهت هماهنگی ، پاسخگویی وجمع آوری انواع اطلاعات
2- تعریف مکانیزم های گزارش حملات
جمع بندی :
مهندسی اجتماعی یکی از آسان ترین و در عین حال پر زیان ترین راههای نفوذ در شبکه های سازمانها می باشد . با این حال به نظر می رسد هنوز فرهنگ ایمن سازی شبکه در مقابل سوء استفاده از نیروی انسانی آن طور که باید وشاید بوجود نیامده است .بدیهی است در این راه پیشگیری بهتر از درمان بوده وبی شک آموزش کارکنان سازمان به عنوان عوامل اصلی مورد حمله، مهمترین مرحله پیشگیری محسوب می گردد.
فهرست منابع وموُاخذ :
1- سایت ویکی پدیا en.wikipedia.org
2-سایت شرکت سخا روش www.Srco.ir
3- سایت پرشین هک www.Persianhack.com
4- مبانی مهندسی اجتماعی از سایت .com ww.Securityfocus
گردآورنده ومترجم : مهسا سمواتی - کارشناس ارشد اتوماسیون اداری) امور بهره وری شرکت ملی پالایش وپخش)
واژگان کلیدی : مهندسی اجتماعی - امنیت شبکه - Social Engineering - Phishing - LAN Security
 نوشته شده توسط علی در چهارشنبه 90/1/31 و ساعت 8:56 صبح | نظرات دیگران()
نوشته شده توسط علی در چهارشنبه 90/1/31 و ساعت 8:56 صبح | نظرات دیگران()مفهوم منطق فازی (Fuzzy logic) اولین بار در پی تنظیم نظریه مجموعههای فازی به وسیله پروفسور لطفی زاده (1965 م) در صحنه محاسبات نو ظاهر شد.
دانش مورد نیاز برای بسیاری از مسائل مورد مطالعه به دو صورت متمایز ظاهر میشود:
1. دانش عینی مثل مدلها، و معادلات، و فورمولهای ریاضی که از پیش تنظیم شده و برای حل و فصل مسائل معمولی فیزیک، شیمی، یا مهندسی مورد استفاده قرار میگیرد.
2. دانش شخصی مثل دانستنیهایی که تا حدودی قابل توصیف و بیان زبانشناختی بوده، ولی، امکان کمی کردن آنها با کمک ریاضیات سنتی معمولاً وجود ندارد.
از آن جا که در عمل هر دو نوع دانش مورد نیاز است منطق فازی میکوشد آنها را به صورتی منظم، منطقی، و ریاضیاتی بایکدیگر هماهنگ گرداند.
منطق فازی از جمله منطقهای چندارزشی بوده، و بر نظریه مجموعههای فازی تکیه میکند. مجموعههای فازی خود از تعمیم و گسترش مجموعههای قطعی به صورتی طبیعی حاصل میآیند.
مجموعههای قطعی (Crisp sets) در واقع همان مجموعههای عادی و معمولی هستند که در ابتدای نظریه کلاسیک مجموعهها معرفی میشوند. افزودن صفت قطعی به واقع وجه تمایزی را ایجاد مینماید که به کمک آن میشود یکی از مفاهیم ابتکاری و حیاتی در منطق فازی موسوم به تابع عضویت را به آسانی در ذهن به وجود آورد.
در حالت مجموعههای قطعی، تابع عضویت فقط دو مقدار در برد خود دارد:
آری و خیر (یک و صفر) که همان دو مقدار ممکن در منطق دوارزشی کلاسیک هستند. بنابراین:
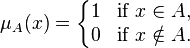
که در اینجا  تابع عضویت عنصر x در مجموعه قطعی A است.
تابع عضویت عنصر x در مجموعه قطعی A است.
برد تابع عضویت از {0,1} در مورد مجموعههای قطعی به بازه بسته [0,1] برای مجموعههای فازی تبدیل میشود.
متغیرهای زبانی به متغیرهایی گفته میشود که مقادیر مورد قبول برای آنها به جای اعداد، کلمات و جملات زبانهای انسانی یا ماشینی هستند. همچنین که در محاسبات ریاضی از متغیرهای عددی استفاده میگردد در منطق فازی نیز از متغیرهای زبانی (گفتاری یا غیر عددی) استفاده میگردد متغیرهای زبانی بر اساس ارزشهای زبانی (گفتاری) که در مجموعه عبارت(کلمات /اصطلاحات) قرار دارند بیان میشود:عبارت زبانی(گفتاری Linguistic terms) صفاتی برای متغیرهای زبانی هستند. به عنوان مثال متغیر زبانی «سن» بسته به تقسیمات مورد نظرشخصی وشرایط میتواند مجموعه عبارت از قبیل «نوجوان»، «جوان»، «میان سال»، «سالمند» باشد: مجموعه عبارات (اصطلاحات)فازی (سن) = { «جوان»، «نه جوان»، «نه چندان جوان»، «خیلی جوان»، ...، «میان سال»، «نه چندان میان سال»، ...، «پیر»، «نه پیر»، «خیلی پیر»، «کم و بیش پیر»، ...، «نه خیلی جوان و نه خیلی پیر»، «نه جوان و نه پیر»... }
یا مثال دیگر، فشار(خون) را میشود متغیری زبانی در نظر گرفت، که ارزشهای (خصوصیتهای)از قبیل پایین، بالا، ضعیف، متوسط، و قوی را میتواند در خود جای دهد. به زبان ریاضی داریم (T = Terms):
{پایین، بالا، ضعیف، متوسط، قوی} = (فشار)T
صفت عدم قطعیت، به صور گوناگون، در همه زمینهها و پدیدهها صرف نظر از روش شناسی مورد کاربرد جهت مطالعه، طراحی، و کنترل پدیدار میشود.
برای مقابله مؤثر با پیچیدگی روزافزون در بررسی، مطالعه، مدلسازی، و حل مسائل جدید در فیزیک، مهندسی، پزشکی، زیست شناسی، و بسیاری از امور گوناگون دیگر ایجاد و ابداع روشهای محاسباتی جدیدی مورد نیاز شدهاست که بیشتر از پیش به شیوههای تفکر و تعلم خود انسان نزدیک باشد. هدف اصلی آنست که تا حد امکان، رایانهها بتوانند مسائل و مشکلات بسیار پیچیده علمی را با همان سهولت و شیوایی بررسی و حل و فصل کنند که ذهن انسان قادر به ادراک و اخذ تصمیمات سریع و مناسب است.
در جهان واقعیات، بسیاری از مفاهیم را آدمی به صورت فازی (fuzzy به معنای غیر دقیق، ناواضح، و مبهم) درک میکند و به کار میبندد. به عنوان نمونه، هر چند کلمات و مفاهیمی همچون گرم، سرد، بلند، کوتاه، پیر، جوان، و نظائر اینها به عدد خاص و دقیقی اشاره ندارند، ذهن انسان با سرعت و با انعطاف پذیری شگفتآوری همه را میفهمد و در تصمیمات و نتیجه گیریهای خود به حساب میگیرد. این، در حالی ست که ماشین فقط اعداد را میفهمد و اهل دقّت است. اهداف شیوههای نو در علوم کامپیوتر آن است که اولا رمز و راز اینگونه تواناییها را از انسان بیاموزد و سپس آنها را تا حد امکان به ماشین یاد بدهد.
قوانین علمی گذشته در فیزیک و مکانیک نیوتونی همه بر اساس منطق قدیم استوار گردیدهاند. در منطق قدیم فقط دو حالت داریم: سفید و سیاه، آری و خیر، روشن و تاریک، یک و صفر، و درست و غلط. متغیرها در طبیعت یا در محاسبات بر دو نوعند: ارزشهای کمی که میتوان با یک عدد معین بیان نمود و ارزشهای کیفی که براساس یک ویژگی بیان میشود. این دو ارزش قابل تبدیلند:
مثلا در مورد قد افراد با ارزش عددی (سانتیمتر)اندازهگیری شود و افراد را به دستههای قدکوتاه و قدبلند تقسیمبندی کنیم و حد آستانه 180 سانتیمتر برای قد بلندی مدنظر باشد. تمامی افراد زیر 180 سانتی متر براساس منطق قدیم قدکوتاهند حتی اگر قد فرد 179 سانتیمتر باشد. ولی در مجموعه فازی هر یک از این صفات براساس تابع عضویت تعریف و بین صفر تا یک ارزشگذاری میشود. از آن جا که ذهن ما با منطق دیگری کارهایش را انجام میدهد و تصمیماتش را اتّخاذ میکند، جهت شروع، ایجاد و ابداع منطقهای تازه و چندارزشی مورد نیاز است که منطق فازی یکی از آنها میباشد.
تفاوت نظریه فازی و نظریه احتمالات:
 نوشته شده توسط لادن در دوشنبه 90/1/29 و ساعت 10:2 صبح | نظرات دیگران()
نوشته شده توسط لادن در دوشنبه 90/1/29 و ساعت 10:2 صبح | نظرات دیگران()شبکههای عصبی مصنوعی (Artificial Neural Network - ANN) یا به زبان سادهتر شبکههای عصبی سیستمها و روشهای محاسباتی نوینی هستند برای یادگیری ماشینی، نمایش دانش، و در انتها اعمال دانش به دست آمده در جهت بیشبینی پاسخهای خروجی از سامانههای پیچیده. ایده اصلی این گونه شبکهها (تا حدودی) الهامگرفته از شیوه کارکرد سیستم عصبی زیستی، برای پردازش دادهها، و اطلاعات به منظور یادگیری و ایجاد دانش قرار دارد. عنصر کلیدی این ایده، ایجاد ساختارهایی جدید برای سامانه پردازش اطلاعات است. این سیستم از شمار زیادی عناصر پردازشی فوق العاده بهمپیوسته با نام نورون تشکیل شده که برای حل یک مسأله با هم هماهنگ عمل میکند.
با استفاده از دانش برنامهنویسی رایانه میتوان ساختار دادهای طراحی کرد که همانند یک نرون عمل نماید. سپس با ایجاد شبکهای از این نورونهای مصنوعی به هم پیوسته، ایجاد یک الگوریتم آموزشی برای شبکه و اعمال این الگوریتم به شبکه آن را آموزش داد.
این شبکهها برای تخمین (Estimation) و تقریب (Approximation)کارایی بسیار بالایی از خود نشان داده اند. گستره کاربرد این مدلهای ریاضی بر گرفته از عملکرد مغز انسان، بسیار وسیع میباشد که به عنوان چند نمونه کوچک می توان استفاده از این ابزار ریاضی در پردازش سیگنالهای بیولوییکی، مخابراتی و الکترونیکی تا کمک در نجوم و فضا نوردی را نام برد.
اگر یک شبکه را همارز با یک گراف بدانیم، فرآیند آموزش شبکه تعیین نمودن وزن هر یال و bias اولیه خواهد.
 نوشته شده توسط لادن در دوشنبه 90/1/29 و ساعت 9:51 صبح | نظرات دیگران()
نوشته شده توسط لادن در دوشنبه 90/1/29 و ساعت 9:51 صبح | نظرات دیگران()مسئله چند وزیر یک معمای شطرنجی و ریاضیاتی است که بر اساس آن باید n وزیر شطرنج در یک صفحه n×n شطرنج بهگونهای قرار داده شوند که هیچیک زیر ضرب دیگری نباشند. با توجه به اینکه وزیر بهصورت افقی، عمودی و اُریب حرکت میکند، باید هر وزیر را در طول، عرض و قطر متفاوتی قرار داد.
اولین و مشهورترین شکل این مسئله معمای هشت وزیر است که برای حل آن باید 8 وزیر را در یک صفحهً معمولی (8x8) شطرنج قرار داد. این مسئله 92 جواب دارد که 12 جواب آن منحصر بهفرد است یعنی بقیه جوابها از تقارن جوابهای اصلی بهدست میآید.
مسئله n وزیر در صورتی جواب دارد که n مساوی 1 یا بیشتر از 3 باشد. یعنی مسئله دو وزیر و سه وزیر راه حلی ندارند.
این مسئله در سال 1848 توسط شطرنج بازی به نام Max Bezzel عنوان شد و ریاضی دانان بسیاری ازجمله Gauss و Georg Cantor بر روی این مسئله کار کرده و در نهایت آنرا به n وزیر تعمیم دادند. اولین راه حل توسط Franz Nauck در سال 1850 ارائه شد که به همان مسئله n وزیر تعمیم داده شد. پس از آن Gunther راه حلی با استفاده از دترمینان ارائه داد که J.W.L. Glaisher آنرا کامل نمود.در سال 1979، Edsger Dijkstra Nauck با استفاده از الگوریتم عقب گرد اول عمق، این مسئله را حل کرد.
هدف از مسئله n وزیر، چیدن n مهره وزیر در یک صفحه شطرنج(n*n) است، به طوری که هیچ دو وزیری یکدیگر را گارد ندهند، یعنی هیچ دو مهرهای نباید در یک سطر، ستون یا قطر یکسان باشند.وزیر در خانههای شطرنج به صورت عرضی، طولی و قطری میتواند حرکت کند. مسئله n وزیر از جمله مسائل NP در هوش مصنوعی است که روشهای جستجوی معمولی قادر به حل آنها نخواهد بود
از تکنیک عقبگرد Backtracking برای حل مسائلی استفاده میشود که در آنها دنبالهای از اشیاء از یک مجموعه مشخص انتخاب میشود، به طوری که این دنباله، ملاکی را در بر میگیرد.عقبگرد حالت اصلاح شده? جست و جوی عمقی یک درخت است.این الگوریتم همانند جست و جوی عمقی است، با این تفاوت که فرزندان یک گره فقط هنگامی ملاقات میشوند که گره امید بخش باشدو در آن گره حلی وجود نداشته باشد. با توجه به اینکه هیچ ? وزیری نباید همدیگر را گارد کنند و در یک سطر نمیتوانند باشند، تعداد کل حالتها برای n=? برابر ?*?*?*?=??? است. در شطرنج یک وزیر میتواند به مهرههایی که در خانههای عمود یا مورب به وی قرار دارند حمله کند. یا به عبارت ریاضی، اگر ردیفها و ستونهای شطرنج را از یک تا هشت شماره گذاری کنیم و وزیر در خانه (i, j) قرار داشته باشد، مهرههایی که در خانههای (i, m) یا (m, j) یا (i ± m, j ± m) قرار دارند توسط وزیر تهدید میشوند.
برای سادگی تشریح این مسئله با استفاده از روش بازگشت به عقب، فرض میکنیم که خانههای شطرنج 4x4و تعداد وزیرها نیز 4 باشد. سپس بعد از یافتن راه حل برای این مسئله ساده شده، اقدام به نوشتن الگوریتم برای مسئله اصلی میکنیم.
مراحل جستجو برای یافتن جواب را به این صورت دنبال میکنیم که: وزیر اول را در ردیف اول و ستون اول قرار میدهیم.
در ردیف دوم از اولین ستون به جلو رفته و به دنبال خانهای میگردیم که مورد تهدید وزیر اول نباشد و وزیر دوم را در این خانه قرار میدهیم.
همانند قبل، در ردیف سوم از اولین ستون به جلو رفته و به دنبال خانهای میگردیم که مورد تهدید وزیران اول و دوم نباشد. میبینیم که چنین خانهای موجود نیست. پس به عقب یعنی ردیف دوم برگشته و وزیر دوم را به خانهای دیگر از ردیف دوم منتقل میکنیم که مورد تهدید وزیر اول نباشد.
دوباره در ردیف سوم اولین خانهای را میابیم که مورد تهدید دو وزیر قبلی نباشد. این بار خانه را مییابیم و وزیر سوم را در آن قرار میدهیم.
همانند قبل، در ردیف چهارم به دنبال اولین خانهای میگردیم که مورد تهدید وزیران پیشین نباشد. چنین خانهای موجود نیست. به ردیف قبل یعنی ردیف سوم باز میگردیم تا خانهای دیگر برای وزیر سوم بیابیم. خانه دیگری وجود ندارد. به ردیف قبل یعنی ردیف دوم بر میگردیم تا خانه دیگری برای وزیر دوم پیدا کنیم. به آخرین ستون رسیدهایم و خانه دیگری نیست. به ردیف قبل یعنی ردیف اول بر میگردیم و وزیر اول را یک ستون به جلو میبریم.
در ردیف دوم اولین خانهای را میابیم که مورد تهدید وزیر اول نباشد و وزیر دوم را در آن خانه قرار میدهیم.
در ردیف سوم اولین خانهای را میابیم که مورد تهدید وزیران اول و دوم نباشد و وزیر سوم را در آن خانه میگذاریم.
در ردیف چهارم اولین خانهای را میابیم که مورد تهدید وزیران پیشین نباشد. این بار خانه را مییابیم و وزیر چهارم را در آن خانه قرار میدهیم.
به یک جواب میرسیم. حال اگر فرض کنیم که این خانه جواب نیست و به مسیر خود ادامه دهیم، احتمالا" میتوانیم جوابهای دیگری نیز بیابیم.
void queens ( index i)
{
index j;
if ( promising(i))
if ( i == n)
cout << col [1] through col [n];
else
for ( j = 1 ; j ≤ n ; j++ ) {
col [ i +? ] = j;
queens ( i + 1);
}
}
bool promising ( index i )
{
index k ;
bool switch;
k = ?;
switch = true ;
while ( k < i && switch ) {
if (col [i] == col[k] || abs(col[i] – col[k] == i-k)
switch = false;
k++;
}
return switch;
}
#include <stdio.h>
int b[?];
inline static int unsafe(int y) {
int i, t, x;
x = b[y];
for (i = ?; i <= y; i++) {
t = b[y - i];
if ( (t == x) ||
(t == x - i) ||
(t == x + i) ) {
return 1;
}
}
return 0;
}
static void putboard(void) {
static int s = ?;
int x, y;
printf("\n\nSolution #?i\n", ++s);
for (y = ?; y < ?; y++) {
for (x = ?; x < ?; x++) {
printf((b[y] == x) ? "|Q" : "|_");
}
printf("|\n");
}
}
int main(void) {
int y = 0;
b[?] = -1;
while (y >= 0) {
do {
b[y]++;
} while ((b[y] < 8) && unsafe(y));
if (b[y] < 8) {
if (y < 7) {
b[++y] = -1;
} else {
putboard();
}
} else {
y--;
}
}
return 0;
}
#include <assert.h>
#include <stdio.h>
#define MAXSIZE 8
class EightQueens
{
int m_size;
int m_solution_count;
int m_attempt_count;
int m_queen[MAXSIZE];
bool m_row_inuse[MAXSIZE];
bool m_diag_rise[MAXSIZE*2];
bool m_diag_fall[MAXSIZE*2];
public:
EightQueens(int size, bool is_alt) {
assert(size <= MAXSIZE);
m_size = size;
m_solution_count = 0;
m_attempt_count = 0;
for (int i = 0; i < m_size; i++) {
m_queen[i] = i;
m_row_inuse[i] = 0;
}
for (int j = 0; j < m_size*2; j++) {
m_diag_rise[j] = 0;
m_diag_fall[j] = 0;
}
if (is_alt) SearchAlt(0);
else Search(0);
}
int GetSolutionCount() {
return m_solution_count;
}
int GetAttemptCount() {
return m_attempt_count;
}
private:
void SearchAlt(int col){
if (col == m_size) {
m_solution_count++;
return;
}
for (int row = 0; row < m_size; row++) {
m_attempt_count++;
if (m_row_inuse[row] == 0 && IsDiagValid(col, row)) {
m_queen[col] = row;
m_row_inuse[row] = 1;
SetDiags(col, 1);
SearchAlt(col+1);
SetDiags(col, 0);
m_row_inuse[row] = 0;
m_queen[col] = -1;
}
}
}
void Search(int col) {
if (col == m_size) {
m_solution_count++;
return;
}
for (int i = col; i < m_size; i++) {
if (SwapQueenIfDiagValid(col, i)) {
Search(col+1);
UnSwapQueen(col, i);
}
}
}
void SwapQueenBasic(int i, int j) {
int hold = m_queen[i];
m_queen[i] = m_queen[j];
m_queen[j] = hold;
}
void SetDiags(int col, int val) {
assert(m_diag_rise[m_queen[col] + col] != val);
m_diag_rise[m_queen[col] + col] = val;
assert(m_diag_fall[m_queen[col] - col + m_size] != val);
m_diag_fall[m_queen[col] - col + m_size] = val;
}
bool IsDiagValid(int col, int row) {
return (m_diag_rise[row + col] == 0 &&
m_diag_fall[row - col + m_size] == 0);
}
bool SwapQueenIfDiagValid(int i, int j) {
m_attempt_count++;
if (IsDiagValid(i, m_queen[j])) {
SwapQueenBasic(i, j);
SetDiags(i, 1);
return true;
}
return false;
}
void UnSwapQueen(int i, int j) {
SetDiags(i, 0);
SwapQueenBasic(i, j);
}
};
void
do_work(bool is_alt)
{
int size = 8;
EightQueens puzzle(size, is_alt);
int soln = puzzle.GetSolutionCount();
int attempt = puzzle.GetAttemptCount();
assert(size != 8 || soln == 92);
const char* style = is_alt ? "cartesian" : "permutation";
printf("EightQueens[%d] has %d solutions found in %5d attempts using %s search.\n", size, soln, attempt, style);
}
int main()
{
printf("We should have 92 solutions for 8x8.\n");
do_work(0);
do_work(1);
}
از الگوریتم مونت کارلو برای برآورد کردن کارایی یک الگوریتم عقبگرد استفاده میشود.الگوریتمهای مونت کارلو، احتمالی هستند، یعنی دستور اجرایی بعدی گاه به طور تصادفی تعیین میشوند.در الگوریتم قطعی چنین چیزی رخ نمیدهد.الگوریتم مونت کارلو مقدار مورد انتظار یک متغیر تصادفی را که روی یک فضای ساده تعریف میشود، با استفاده از مقدار میانگین آن روی نمونه تصادفی از فضای ساده بر آورد میکند.تضمینی وجود ندارد که این برآورد به مقدار مورد انتظار واقعی نزدیک باشد، ولی احتمال نزدیک شدن آن، با افزایش زمان در دسترس برای الگوریتم، افزایش مییابد.
int ostimate _ n_ queens (int n)
{
index i , j , col [1..n];
int m , mprod , numnodes ;
set _of_ index prom _children;
i = 0;
numnodes =1 ;
m = 1;
mprod = 1;
while ( m != 0 && i != n ) {
mprod = mprod * m ;
numnodes = numnodes + mprod * n;
i ++;
m = 0 ;
prom_childern = Ø;
for ( j = 1 ; j ≤ n ; j++;) {
col [i] = j ;
if ( promising(i)) {
m++;
prom_children = prom _ children U {i};
}
}
if ( m != 0) {
j = random selection from prom _childeren;
col [i];
}
}
return numnodes;
}
برای حل این مسئله که دارای 92 جواب است، باید تکنیکهایی جهت کاهش حالات، روش Brute Force یا امتحان تک تک جوابها انجام شود. تعداد همه حالاتی که میتواند در روش Brute Force چک شود برابر 16،777،216یا هشت به توان هشت است! یکی از روشهای حل این مسئله برای n>=4 یا n=1 استفاده از روش مکاشفهای ( heuristic)است:
1- عدد n را بر عدد 12 تقسیم کن و باقی مانده را یادداشت کن
2- به ترتیب اعداد زوج 2 تا n را در لیستی بنویس
3- اگر باقی مانده 3 یا 9 بود، عدد 2? را به انتهای لیست انتقال بده.
4- به لیست اعداد فرد ? تا n را به ترتیب اضافه کن، اما اگر باقی مانده 8 بود اعداد را دو به دو باهم عوض کند (مثلا1و3و5و7و9 تبدیل به 3و1و5و7و9 میشه)
5- اگر باقی مانده 2 بود جای 1و3 را با هم عوض کن و 5 را به انتهای لیست ببر.
6- اگر باقی مانده 3 یا 9 بود، اعداد 1و 3را به انتهای لیست ببر.
7- حال با استفاده از لیست بدست آمده وزیرها در صفحه شطرنج چیده میشوند، بطوریکه جای وزیر ستون اول، اولین عدد لیست، جای وزیر ستون دوم، دومین عدد لیست و ...
این الگوریتم یک راه حل برای حل این مسئلهاست، برای بدست آوردن همه حالات از روشهای دیگری میتوان استفاده کرد. روش حل مسئله 12 راه حل یکتا دارد که با در نظر گیری تقارن و چرخش به 99 حالت قابل تبدیل است.
میتوان به مسئله 8 وزیر به عنوان یک مسئله بهینه سازی نیز نگریست که در آن هدف بهینه کردن تعداد گاردهای جفت وزیرها میباشد.
به عنوان مثال فرض کنید در صفحه شطرنج معمولی ،8 وزیر را به دو روش زیر قرار دهیم :


در روش چینش سمت چپ 3 وزیر و در روش چینش سمت راست 4وزیر همدیگر را گارد میدهند. بنابراین روش چینش قبلی بهینه تر از روش چینش فعلی است. در واقع میتوان مسئله بهینه سازی را به صورت زیر تعریف کرد. فرض کنید S مجموعه همه جوابهای ممکن برای مسئله باشد. در صورتی S* میتواند جواب مسئله باشد که به ازای همه جوابهای موجود در S ، S* بهینه تر از دیگر جوابها باشد. در مسئله 8وزیر دیدیم که جوابی بهینهاست که تعداد گاردهای جفت وزیر آن کمتر باشد.
روشهای جستجوی محلی همگی حالتهای همسایه حالت فعلی را برای رسیدن به بهینهترین جواب بررسی میکنند. از این رو وجود دو تابع در همه این روشهای جستجو الزامی است. اولین تابع میزان بهینگی جواب مسئله ارزیابی میکند و تابع دوم یکی از حالتهای همسایه حالت فعلی را انتخاب میکند.
نحوه پیاده سازی و طراحی الگوریتم برای انتخاب حالت هسایه در این روشهای جستجو از اهمیت ویژهای برخوردار است. به عنوان مثال برای مسئله 8 وزیر میتوان به شکلهای زیر حالتهای همسایگی را تولید کرد:
1) دو وزیر به تصادف انتخاب شده و جای آن دو باهم عوض گردد.
2) یکی از وزیرها به تصادف انتخاب شده و شماره سطر آن به تصادف تغییر کند.
3) ویزیری به تصادف انتخاب شده و یک خانه به سمت بالا یا پایین حرکت کند
Eight queens puzzle. (2010, May 3). In Wikipedia, The Free Encyclopedia. Retrieved 18:33, May 7, 2010,
 نوشته شده توسط لادن در یکشنبه 90/1/28 و ساعت 3:49 عصر | نظرات دیگران()
نوشته شده توسط لادن در یکشنبه 90/1/28 و ساعت 3:49 عصر | نظرات دیگران()ارتباط با یک کامپیوتر از راه دور بوسیله مودم
اگر دو کامپیوتر در دو نقطه دنیا داشته باشیم که هر دو داری مودم و همچنین یک خط تلفن باشند با تنظیمات زیر در ویندوز وبدون هیچ نرم افزاری و بدون استفاده از اینترت و شبکه داخلی میتوان با هم دیگر ارتباط داشته باشند و از راه دور با ان کامپیوتر کار کرد
تنظیمات کامپیوتر میزبان که به آن می خواهید از را دور وصل شوید
تنظیمات کامپیوتر مهمان که بوسیله آه ما می خواهیم به کامپیوتر میزبان که در مکان دیگر است می خواهیم وصل شویم
بعد از وصل شدن میتونید از برنامه Remote Desktop که در ویندوز موجود هست استفاده کنید و در قسمت IP اون ، IP کامپیوتر منزلتون رو وارد کنید( 192.168.1.3 )
 نوشته شده توسط علی در جمعه 90/1/26 و ساعت 2:32 عصر | نظرات دیگران()
نوشته شده توسط علی در جمعه 90/1/26 و ساعت 2:32 عصر | نظرات دیگران()